#240 – Pitot Gauges: How Do I Calculate the PSI to GPM Conversion?

Follow these simple steps to ensure fire hydrants can deliver adequate water flow during a fire

Firefighting operations can be seriously jeopardized if fire hydrants aren’t ready and able to deliver the required water flow and pressure. Municipalities and other authorities insist upon regular hydrant flow testing to ensure that adequate water is available when it’s needed most—which is where pitot gauges come in.

In theory, pitot gauges make it simple to measure the flow of fire hydrants and convert readings in pounds per square inch (PSI) to gallons per minute (GPM), enabling inspectors to quickly uncover reduced flow rates. But in reality, the equation and chart can be confusing—and QRFS phones are constantly ringing with the question: How do I do this right?

In this blog, we will take you step-by-step through the process of converting a pitot gauge’s PSI reading to GPM. We promise that we’ll make it so simple even your grandmother could do it accurately—especially since we’ve provided a calculator to help you make the conversion. Feel free to jump straight to the formula, followed by a step-by-step process and a calculator.

In the market for pitot gauges? Be sure to browse our selection of pitot gauge kits and accessories, including our best-selling Inspector’s Choice Pitot Gauge Kit, which costs a little more but delivers 1 percent full-range accuracy.

Pitot gauge 101: here’s how they work

Fire hydrants are color-coded according to their strength of output, enabling fire departments to assess their water resource capabilities quickly when they arrive on the scene of an emergency. For instance, red hydrants typically have a rated capacity of less than 500 GPM and light blue hydrants have a rated capacity of more than 1,500 GPM. With so much at stake, it’s critical for hydrants to perform as expected during a fire.

A handheld pitot gauge is the quickest, simplest method for measuring straight-tip and hydrant-flow GPM. Analyzing the data it collects can also reveal heavy pipe-wall deposits and closed valves that can significantly impede a hydrant’s pressure and flow.

Previously, we’ve offered a detailed guide on how to use a pitot gauge for hydrant flow testing. But here’s a quick overview of how pitot gauges work:

A pitot gauge consists of three components: a blade, handle, and pressure gauge. After it’s inserted into an open fire hydrant’s water discharge, a narrow tube inside the blade directs water toward the gauge to create a pressure reading. Generally, the edge of the blade is set parallel to the direction of fluid-stream movement, at a distance about one-half the diameter of the opening in the center of the stream. Put simply, that means if the orifice is 2.5 inches, the blade should be about 1.25 inches out.

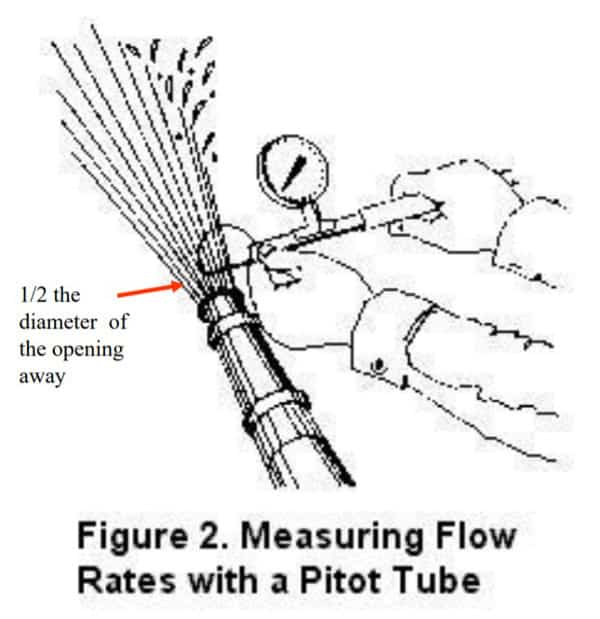
The captured PSI readings from a group of hydrants in the same vicinity are then used to calculate the disparities in pressure between two points along the distribution system. But in order to understand the results, the PSI readings need to be converted to GPM, the standard measurement of water flow. And that’s where it gets a little tricky.

PSI can’t be directly converted to GPM; these are two different units of measure. PSI measures pressure and GPM measures flow rate.

But if other variables are known, the water’s flow rate in GPM can be calculated with the help of the Bernoulli equation for incompressible fluid and careful unit conversion. Bernoulli, a Swiss mathematician, developed a formula that represents the relationship between velocity and pressure along a streamline.

Bernoulli’s original equation must be modified so that it accounts for the friction produced when water flows through a hydrant. When represented mathematically, the friction is called the “hydrant’s coefficient” and is determined by the loss in flow caused by the hydrant’s internal orifice design.

The formula: what do all those variables mean?

After successfully completing the flow test and recording the information, here’s the formula used to determine the rate of discharge flowing from a single fire hydrant in GPM:

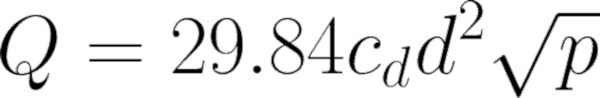
Let’s break down what those variables mean:

• 29.84 is a constant derived from physical laws relating to water velocity, pressure, and conversion factors. In short, this number keeps the answer in GPM. Some sources offer a slightly smaller constant of 29.83.
• c_d = the coefficient of discharge, which represents friction loss.
• d = the actual inside diameter of the hydrant orifice in inches.
• p = the pressure in PSI read at the orifice by the pitot gauge. Because this formula takes the square root of p—rather than p itself—large increases in PSI will have a fairly small impact on the final GPM.
• Q = a number used to represent the result, or discharge in GPM.

Finding the numbers to plug in for “d” and “p” are easy. To determine d, simply measure the inside diameter of the hydrant’s outlet or outlet nozzle where flow occurs; to find p, record the pitot gauge reading.

The discharge coefficient, or “c,” varies with the type of outlet on the hydrant. Different manufacturers have different internal hydrant orifice designs, and friction is created as water is required to go around bends or sharp corners.

In most modern hydrants, the transition between the vertical barrel of the hydrant and the horizontal outlet is smooth and rounded. In the diagram below, consider the difference between the transitions (which look like wings on either side of the middle rectangle) in the first two outlet drawings. The rounded design has a coefficient of 0.9, meaning there is only a 10 percent decline in water flow due to friction loss.

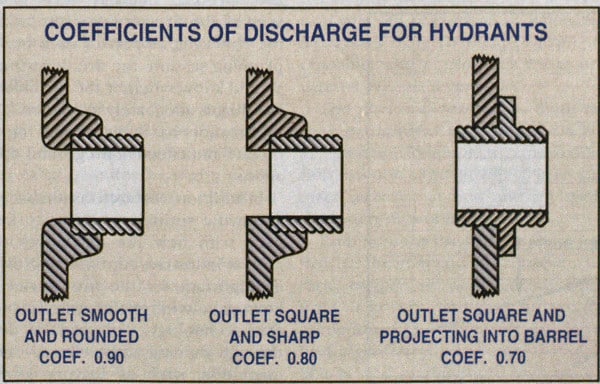
When the transition is square and sharp as in the second drawing, the hydrant has a coefficient of 0.8. When it is square and projects into the barrel of the hydrant like the drawing on the right, the coefficient is 0.7. By poking your fingers inside the outlet, you can determine if it’s smooth and rounded or square and sharp. Compare your findings to the three general types of hydrant outlets in the diagram above to determine the coefficient of discharge.

Practice solving the equation yourself or with our custom hydrant discharge calculator

Now that you understand where the numbers come from, let’s practice solving the equation. While testing a single fire hydrant, here’s what we found:

• The flow reading on the pitot gauge is 62 psi.
• A single 2.5-inch port is used with a measured inside diameter of 2.55 inches. NFPA 291: Recommended Practice For Fire Flow Testing And Marking Of Hydrants recommends using 2.5-inch outlets for flow tests instead of pumper outlets (which are larger than 2.5 inches) because the larger outlets don’t fill completely and provide inaccurate pressure readings. If pumper outlets have to be used, the resulting flow must be modified to account for the voids in water flow.
• The outlet is smooth and rounded, meaning it has a coefficient of 0.9.

So, what’s the total GPM available at normal operating pressure?

Step 1: Multiply the constant 29.84 times the coefficient of discharge (c_d). 29.84 x 0.9 = 26.856

Step 2: Square the measured diameter. 2.55 x 2.55 = 6.5025

Step 3: Multiply those two numbers: 26.856 x 6.5025 = 174.6

Step 4: Find the square root of 62 psi, which is 7.8740

Step 5: Multiply the final two numbers to solve for Q, the discharge in GPM. 174.6 x 7.8740 = 1,375 GPM

Now that you’ve got a grasp on how PSI, discharge coefficients, and diameter impact a hydrant’s flow rates, try our handy GPM calculator for fire hydrants:

Watch this video for another step-by-step example of how to use the pitot gauge’s PSI reading to calculate the rate of water flowing from the hydrant in GPM:

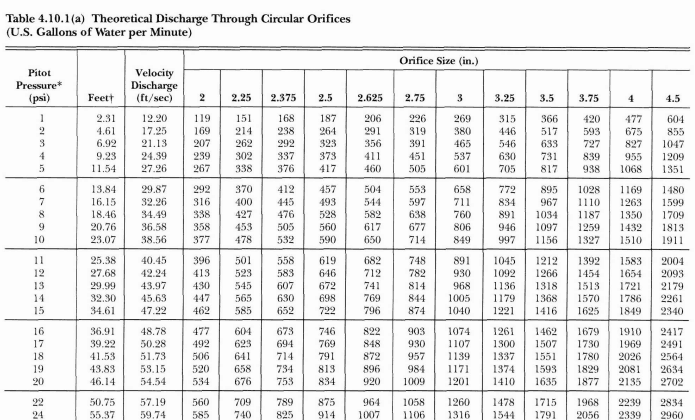
Theoretical discharge tables make converting PSI to GPM even easier

Theoretical discharge tables, like the one we provide with our selection of pitot gauges, make the conversion even simpler. Simply find the pitot pressure reading on the left and slide your finger over to the matching orifice size to reveal the GPM.

But it’s important to keep in mind that the table is based on using a coefficient discharge of 1 in the formula, which is the theoretical discharge from a perfect circular orifice.

In the real world, no orifice is perfect. When more accurate results are required, NFPA 291 explains that the coefficient appropriate for your particular hydrant outlet should be applied to the figures on the table.

In other words, if your pitot pressure is 28 psi and your orifice size is 4, your theoretical discharge according to the table is 2,526 GPM. If the coefficient of your hydrant outlet is 0.9, multiplying 2,526 x 0.9 finds the actual rate of flow: 2,273.4 GPM.

Below is a theoretical discharge table from NFPA 291; it also uses a perfect (impossible) coefficient discharge of 1. Click on the image to see the full-size version:

Pitot gauges help inspectors ensure that fire hydrants are ready and able to fight fires

Pitot gauges are the fastest and easiest way to measure the rate of discharge from fire hydrants – as long as you understand the proper steps to converting pressure readings in pounds per square inch to gallons per minute. Following these simple instructions helps inspectors deliver peace of mind that fire hydrants will perform as expected during a fire.

In the market for pitot gauges? Be sure to browse our selection of pitot gauge kits and accessories, including our best-selling Inspector’s Choice Pitot Gauge Kit, which costs a little more but delivers 1 percent full-range accuracy.

Questions about QRFS products or need a brand or item that’s not in our online inventory? Just call us at +1 (888) 361-6662 or email support@qrfs.com.

This blog was originally posted at blog.qrfs.com. If this article helped you understand fire hydrant testing calculations, check us out at Facebook.com/QuickResponseFireSupply or on Twitter @QuickResponseFS.