Longer dry sprinkler barrels can reduce water flow—but there’s usually no need for custom design calculations
K-factor is an essential part of fire sprinkler system design, as every sprinkler has an orifice through which water flows. The size of this orifice, known as the sprinkler K-factor, determines how quickly water at a given pressure (PSI) and flow (GPM) exit the head. Given that how quickly sprinklers deliver water and how much are key calculations in the design of fire sprinkler systems, understanding K-factor—and purchasing a sprinkler with the exact right one—is crucial.
However, complicating things is that dry sprinklers can have different barrel lengths; longer barrels cause friction that can reduce pressure and flow; and at least some technical data sheets show K-factors that change based on the length of the barrel. So, does this mean that all dry sprinklers require custom design calculations based on their barrel length? Fortunately, no.
Typically, the “nominal K-factor” for a dry sprinkler applies to all barrel lengths. However, there are exceptions referencing “adjusted K-factors.” Read on to learn more, including:
- A bit of math and history behind K-factors
- An explainer of nominal vs. adjusted K-factors and the NFPA 13 rule
Check out QRFS’s wide selection of dry sprinkler heads with standard barrel lengths. To order custom lengths or if you have questions about K-factor considerations, contact our customer service team.
The math (and some physics history) behind sprinkler K-factor
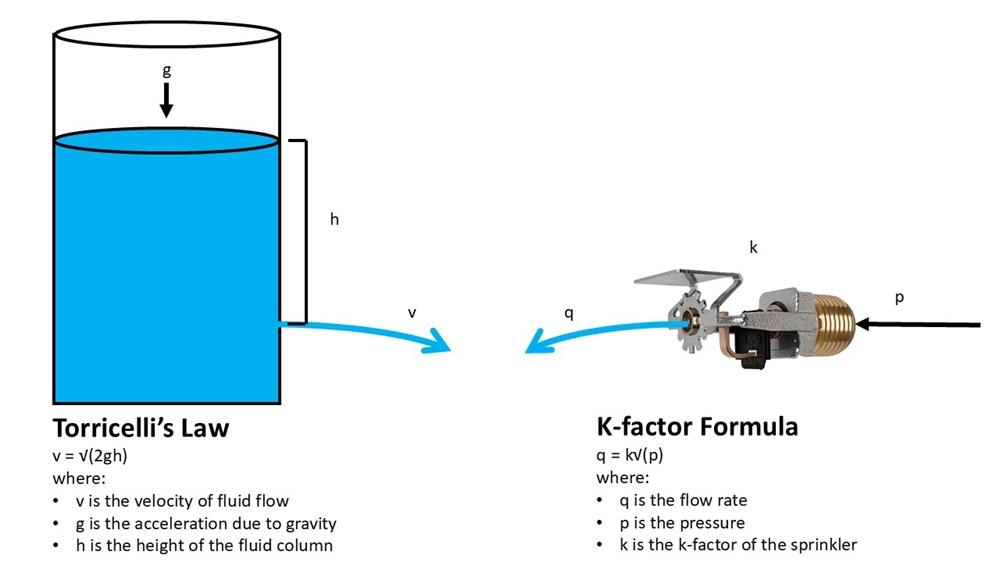
Many people assume that “K-factor” is simply a fancy way of saying “orifice size,” aka “how big the hole is in the sprinkler.” This description is somewhat accurate, but not entirely. The underlying math for the K-factor calculation dates back to 1644 and the work of Italian physicist Evangelista Torricelli, a student of Galileo. Torricelli’s theorem, also called Torricelli’s law, states that the speed of a fluid flowing through a hole varies according to the height of the column of fluid:
v = √(2gh)
Where:
- v is the fluid velocity
- h is the height of the column of fluid
- g is the acceleration due to gravity
For our physicists keeping track at home, this is a special case of Bernoulli’s principle, another key fluid dynamics concept and equation. However, Torricelli’s theorem, as formulated, isn’t quite what’s needed for fire protection system design purposes. Here’s why:
First, we care about the fluid volumetric flow rate in gallons per minute or liters per second, not velocity. Flow rate and velocity are related concepts, but not the same.
Second, Torricelli’s equation is for fluid flowing out of a hole in the bottom of a reservoir, so the only source of pressure is gravity (expressed as 2gh). Instead, we need to express this force in pounds per square inch (PSI) or bar (100,000 Pascals), metrics based on the pressure provided by the system’s water supply, possibly involving a gravity tank or pump.
Finally, Torricelli’s theorem assumes there is a very tiny hole in the reservoir from which the impact of the surface area and any subsequent friction loss are negligible. These are assumptions that can’t be made in fire sprinkler system design. So, for fire protection purposes, the formula is a bit different:
q = k√P
Where:
- q is fluid flow rate
- P is pressure
- k is the K-factor
Side by side, here’s what these concepts look like:
K-factor accounts for the area of the orifice, and variables such as friction loss, turbulence, and the contraction of the fluid stream through a nozzle also play a role in determining how much water sprinklers deliver and how quickly. In particular, friction and turbulence are essential parts of hydraulic calculations for fire sprinkler systems. You can read more about how they work in our previous blog, but here are the basic principles:
- When water flows through pipes, the friction between the water and the pipe material slows down the flow. The longer the pipe and the rougher its material, the more friction.
- When water has to change direction in tees or elbows, turbulence also slows down the flow.
Because fire sprinklers are typically very short and straight nozzles, the effects of friction and turbulence caused by regular heads attached to pipes are generally minimal. However, with dry sprinklers, the length of a very long barrel can affect the flow and the sprinkler’s effective K-factor. Nevertheless, dry sprinklers are often overengineered to account for this impact!
Sprinkler K-factor, dry sprinklers, and barrel length: Nominal vs. adjusted K-factor
One area where the term “K-factor” can certainly mean more than just “orifice size” is dry sprinklers. Used to protect freezing spaces, dry sprinklers have sealed barrels between the sprinkler head and the supply pipe that can reach from a heated compartment into an unheated space. The lengths of barrels on dry sprinklers are customizable, and a given model might be available with barrels (in sizes sometimes referred to as the “A Dimension,” “Order Length,” or another term) anywhere from a couple of inches to several feet.

Generally, unique fire sprinkler models typically only have one possible K-factor. However, with dry sprinklers, having something like four feet of sprinkler barrel between the supply pipe and the hole in the sprinkler seems like it would add an appreciable amount of friction as water passes through. So, how can the R5714 shown above always have a K-factor of 5.6, regardless of whether it’s four inches or four feet long?
It’s because dry sprinklers are overengineered to ensure that every length variation meets the minimum K-factor spec and/or the tested reduction in K-factor due to barrel length in a specific model is minimal. Manufacturers design most dry heads to achieve the nominal K-factor in the longest barrel size. Shorter barrels may overperform by having slightly larger effective K-factors, but slightly more water flow doesn’t cause a significant problem in sprinkler design—whereas too little would. In these cases, a sprinkler’s data sheet may say something like, “Nominal K-factor for all approved lengths,” or simply list one K-factor for that model and be done with it.
However, that is “usually” the situation. Occasionally, a sprinkler manufacturer can publish a list of “degraded” K-factors for different lengths of dry sprinklers. In these cases, specific values listed in the data sheet apply rather than a nominal K-factor. NFPA 13: Standard for the Installation of Sprinkler Systems makes this rule explicit in Chapter 28, Plans and Calculations:
From the 2025 edition of NFPA 13
28.2.4.10.3 Flow from a sprinkler shall be calculated using the nominal K-factor except that the manufacturer’s adjusted K-factors shall be utilized for dry-type sprinklers.
If adjusted K-factors exist for a dry sprinkler, these numbers can be found in the sprinkler’s data sheet in a table like this:
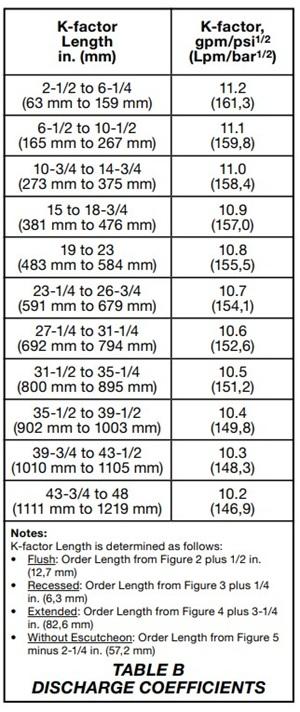
To be clear, manufacturers’ adjusted K-factors are rare. Most dry sprinklers seem to employ the nominal value for all barrel lengths. For example, only two Tyco lines that we are currently aware of—Series DS-2 Dry-Type Sprinklers and Series DS-3 Dry-Type Sprinklers, both 11.2K heads—have adjusted K-factors. Tyco technical support states that it’s because “During the process of testing, extending the barrels showed signs of K-Factor dropping.”
Always check the data sheet for dry sprinkler K-factor
From a physics and fluid dynamics perspective, very long barrels in dry sprinklers cause some flow and pressure losses. But in the vast majority of dry sprinklers, the nominal K-factor is applicable, whereas a few sprinklers will list adjusted K-factors based on barrel length. Verify on the sprinkler’s data sheet!
If you need dry sprinklers, check out QRFS’s huge online selection of models with standard barrel lengths, or contact us to order dry heads with custom barrels.
This blog was originally posted at blog.qrfs.com. If this article helped you, check us out on X @QuickResponseFS.



